💡 Why bother learning Calculus in Robotics?
Predicting, Controlling, and Adapting 🤖
While calculus might stir memories of complex integrals and derivatives from school, it's actually the secret sauce that makes advanced robotics possible. When a robot interacts dynamically with its environment, calculus is there to guide its decisions and actions.
Why is Calculus invaluable?
Control Theory: At the heart of robotics is the desire to control actions seamlessly. Calculus, especially differential equations, helps design control systems that respond effectively to changing conditions.
Rates of Change: Robots need to understand how variables like speed or acceleration change over time. Derivatives in calculus provide this insight, enabling more responsive and adaptive actions.
Predictive Modeling: Whether it's predicting where a thrown ball will land or estimating the movement of an obstacle, calculus helps robots anticipate future scenarios. Integrals can determine accumulated quantities like the total distance travelled.
Calculus isn't just about abstract symbols; it's the framework that allows robots to interact dynamically and predictably with their environment. Through calculus, robots foresee, adapt, and execute with unmatched precision! 📏
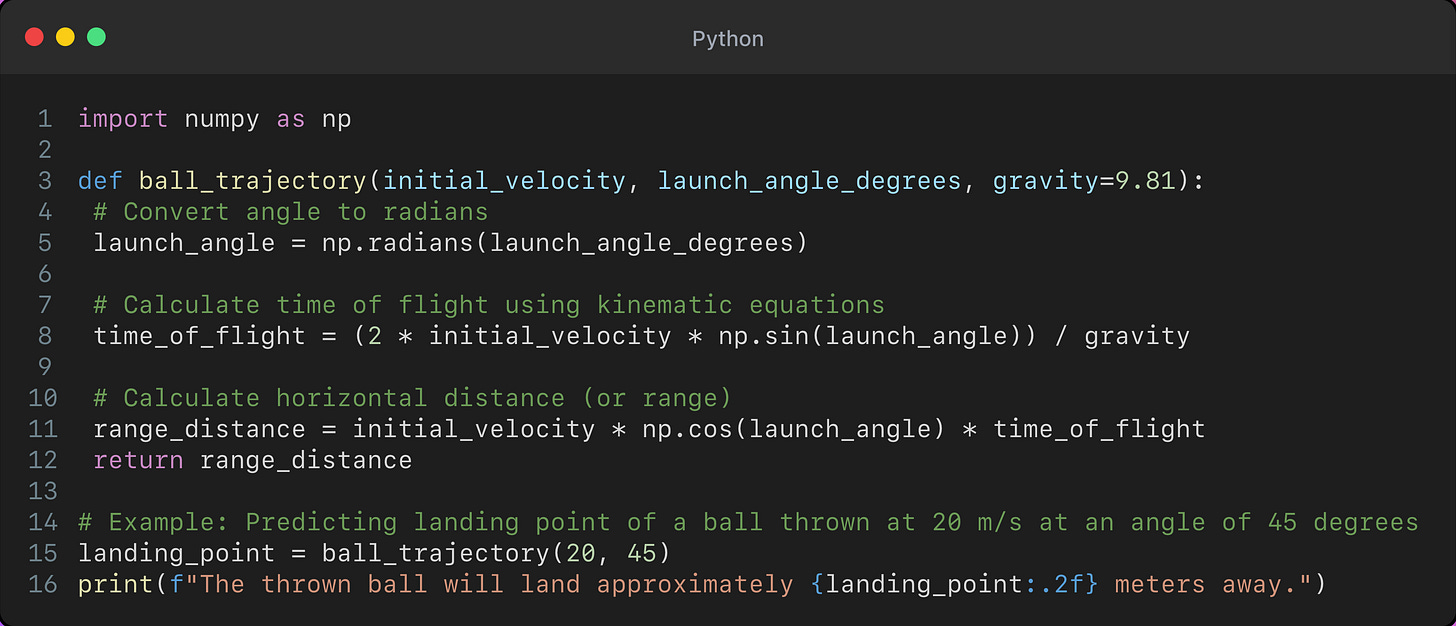
Python Example: Using calculus to estimate where a thrown ball will land:
Real World Example: Robotic Arm in a Manufacturing Assembly Line 🏭
Imagine a robotic arm working on an assembly line in a factory, tasked with picking up parts, placing them accurately, and performing precise operations like welding or screwing.
1. Control Theory:
The robotic arm needs to move from one position to another smoothly and accurately. This movement is governed by control systems that ensure the arm reaches the desired position without overshooting or oscillating.
Calculus, particularly differential equations, is used to design these control systems. For instance, if the arm starts to deviate from its desired path due to an external disturbance, calculus helps in determining the corrective action to bring it back on track.
2. Rates of Change:
As the robotic arm moves, it's essential to know how fast it's moving (speed) and how this speed is changing (acceleration). This is crucial for safety and precision.
Derivatives in calculus provide this information. If the arm needs to slow down as it approaches its target to ensure accurate placement, the derivative will indicate the rate of deceleration required.
3. Predictive Modeling:
Let's say the assembly line occasionally has parts moving on a conveyor belt, and the robotic arm needs to pick them up. The arm must predict where and when the part will be in the optimal position for pick-up.
Calculus aids in this prediction. By analyzing the speed and trajectory of the part on the conveyor, integrals can be used to determine its future position. This allows the robotic arm to time its movement perfectly to pick up the part without any hitches.
Conclusion:
In this example, the robotic arm's efficiency, accuracy, and adaptability are all underpinned by calculus. It ensures that the robot can perform its tasks with precision, respond to changes in its environment, and predict future scenarios to optimize its actions. Without calculus, the robotic arm would struggle to operate seamlessly in a dynamic manufacturing setting.